Bài 21 trang 111 Toán 9 Tập 1

Bài 21 (trang 111 SGK Toán 9 Tập 1): Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Lời giải:

Ta có: AB² + AC² = 3² + 4² = 25

BC² = 5² = 25

Suy ra  AB² + AC² = BC²

=> tam giác ABC vuông tại A hay AC ⊥ BA.

Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

Bài 22 trang 111 Toán 9 Tập 1

Bài 22 (trang 111 SGK Toán 9 Tập 1): Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.

Lời giải:

Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.

Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.

Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.

Bài 23 trang 111 Toán 9 Tập 1

Bài 23 (trang 111 SGK Toán 9 Tập 1): Đố. Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm A, B, C. Chiều quay của đường tròn tâm B ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm A và đường tròn tâm C (cùng chiều quay hay ngược chiều quay của kim đồng hồ).

Lời giải:

Từ hình vẽ, đường tròn (A) và (C) nằm cùng một phía (về bên dưới) so với sợi dây nên có cùng chiều quay, còn đường tròn (B) nằm ở khác phía (bên trên).

=> đường tròn (A) và (C) quay ngược chiều với (B).

Khi dây cua-roa chuyển động, đường tròn (B) quay ngược chiều của kim đồng hồ nên đường tròn (A) và (C) có cùng chiều quay của kim đồng hồ.

Bài 24 trang 111 Toán 9 Tập 1

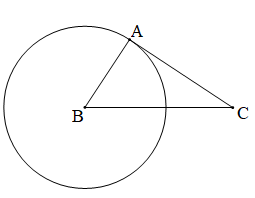
Bài 24 (trang 111-112 SGK Toán 9 Tập 1): Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.

a) Chứng minh rằng CB là tiếp tuyến của đường tròn.

b) Cho bán kính của đường tròn bằng 15cm, AB = 24 cm. Tính độ dài OC.

Lời giải:

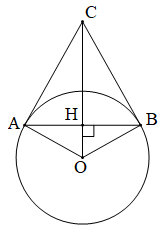
a) Gọi H là giao điểm của OC và AB.

 Tam giác AOB cân tại O (OA = OB, bán kính) có OH là đường cao nên OH cũng là đường phân giác.

Do đó: $$  $$  $$ \widehat{AOC}=\widehat{BOC} $$ .

Xét  $$ \Delta OAC $$  và  $$ \Delta OBC $$  có:

    OA = OB (bán kính) ;

    $$ \widehat{AOC}=\widehat{BOC} $$ ;

    OC cạnh chung

\[\Rightarrow \,\,\Delta OAC=\Delta OBC\left( c.g.c \right)\]  $$ \Rightarrow \,\,\widehat{OBC}=\widehat{OAC}={{90}^{o}} $$ .

Vậy CB là tiếp tuyến của đường tròn (O) (đpcm).

b) Ta có:  $$ AH=\frac{AB}{2}=12\,(cm) $$  (đường kính vuông góc với dây cung).

Áp dụng định lí Pytago trong tam giác vuông OAH:

 $$ OH=\sqrt{O{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{15}^{2}}-{{12}^{2}}}=\sqrt{81}=9\,(cm). $$  

Tam giác OAC vuông tại A, đường cao AH nên \[O{{A}^{2}}=OH.OC\]

\[\Rightarrow \,\,OC=O{{A}^{2}}:OH={{15}^{2}}:9=25\left( cm \right)\].

Bài 25 trang 112 Toán 9 Tập 1

Bài 25 (trang 112 SGK Toán 9 Tập 1): Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b)  Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Lời giải:

a) Bán kính OA vuông góc với BC nên MB = MC.

Lại có MO = MA (theo giả thiết).

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.

Lại có: OA ⊥ BC nên OBAC là hình thoi.

b) Ta có: OA = OB (bán kính)

    OB = BA (tính chất hình thoi).

Nên OA = OB = BA  $$ \Rightarrow  $$  ΔAOB đều  $$ \Rightarrow  $$   $$ \widehat{AOB}={{60}^{o}} $$ .

Trong tam giác OBE vuông tại B ta có:

BE = OB.tg AOB = OB.tg60^o = R. $$ \sqrt{3} $$ .