Bài 10 trang 71 SGK Toán 9 Tập 2

Bài 10 (trang 71 SGK Toán 9 tập 2): a) Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60^o. Hỏi dây AB dài bao nhiêu xentimet?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?

Lời giải

a) Vẽ đường tròn (O ; R. Vẽ góc ở tâm có số đo  $$ {{60}^{o}} $$ .

Góc này chắn cung AB (hình vẽ) và sđ  $$ \overset\frown{AB}={{60}^{o}} $$ .

Ta có  $$ \Delta OAB $$  cân tại O có  $$ \widehat{O}={{60}^{o}} $$   $$ \Rightarrow  $$   $$ \Delta OAB $$  là tam giác đều  $$ \Rightarrow \,\,AB=R=2\,cm. $$

b) Theo câu a), ta có góc ở tâm bằng sđ  $$ \overset\frown{AB}={{60}^{o}} $$ .

Ta có:  $$ {{360}^{o}}:{{60}^{o}}=6 $$  .

Như vậy ta có cách vẽ như sau:

Vẽ 6 dây cung bằng nhau và bằng bán kính R :  $$ {{A}_{1}}{{A}_{2}}={{A}_{2}}{{A}_{3}}={{A}_{3}}{{A}_{4}}={{A}_{4}}{{A}_{5}}={{A}_{5}}{{A}_{6}}={{A}_{6}}{{A}_{1}}=R $$  

 $$ \Rightarrow  $$  6 cung bằng nhau $$ \overset\frown{{{A}_{1}}{{A}_{2}}}=\overset\frown{{{A}_{2}}{{A}_{3}}}=\overset\frown{{{A}_{3}}{{A}_{4}}}=\overset\frown{{{A}_{4}}{{A}_{5}}}=\overset\frown{{{A}_{5}}{{A}_{6}}}=\overset\frown{{{A}_{6}}{{A}_{1}}} $$ .

Bài 11 trang 72 SGK Toán 9 Tập 2

Bài 11 (trang 72 SGK Toán 9 tập 2): Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O') .

a) So sánh các cung nhỏ BC, BD.

b) Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau:  $$ \overset\frown{BE}=\overset\frown{BD} $$ )

Lời giải

a) Xét  $$ \Delta ABC $$  có  $$ OB=OA=OC=\frac{1}{2}AC $$  

 $$ \Rightarrow \,\,\Delta ABC $$  là tam giác vuông tại B  $$ \Rightarrow \,\widehat{ABC}={{90}^{o}} $$ .

Chứng minh tương tự ta có:  $$ \widehat{ABD}={{90}^{o}} $$  

 $$ \Rightarrow \, $$  Ba điểm C, B, D thẳng hàng.

Vì hai đường tròn (O) và (O’) bằng nhau nên AC = AC’ (các đường kính)

 $$  $$   $$ \Rightarrow \,\Delta ACD $$  cân tại A  $$ \Rightarrow  $$  AB là đường cao đồng thời là đường trung tuyến

 $$ \Rightarrow \, $$  B là trung điểm của CD  $$ \Rightarrow \,\,BC=BD\,\,\Rightarrow \overset\frown{BC}=\overset\frown{BD} $$ .

b) Xét đường tròn (O’) có AD là đường kính

 $$ \Rightarrow \,\,EO=O'A=O'D=\frac{AD}{2} $$  

 $$ \Rightarrow \,\,\Delta AED $$  vuông tại E  $$ \Rightarrow \,\,\widehat{AED}={{90}^{o}} $$  hay  $$ \widehat{CED}={{90}^{o}} $$  

Xét tam giác CED vuông tại E có EB là đường trung tuyến ứng với cạnh huyền CD

 $$ \Rightarrow \,\,EB=\frac{1}{2}CD=BC=BD $$   $$ \Rightarrow \,\overset\frown{EB}=\overset\frown{BD} $$ .

Bài 12 trang 72 SGK Toán 9 Tập 2

Bài 12 (trang 72 SGK Toán 9 tập 2): Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD  $$ (H\in BC,\,K\in BD) $$ .

a) Chứng minh rằng OH > OK.

b) So sánh hai cung nhỏ BD và BC.

Lời giải

a) Trong tam giác ABC có  $$ BC<AB+AC $$ .

Mà  $$ AD=AC $$  nên  $$ BC<AB+AD=BD $$ .

Theo định lí về dây cung và khoảng cách từ tâm đến dây ta có:

 $$ BC<BD $$  $$ \Rightarrow \,\,OH>OK $$ .

b) Vì  $$ BC<BD $$  nên  $$ \overset\frown{BC}<\overset\frown{BD} $$ .

Bài 13 trang 72 SGK Toán 9 Tập 2

Bài 13 (trang 72 SGK Toán 9 tập 2): Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Lời giải

+ Trường hợp điểm O nằm ngoài hai dây song song (AB // CD)  (hình vẽ).

Kẻ đường kính MN // AB.

Ta có:  $$ \widehat{MOA}=\widehat{OAB}\,\,;\,\widehat{NOB}=\widehat{OBA} $$  (so le trong)

Mà  $$ \widehat{OAB}=\widehat{OBA} $$  (Vì  $$ \Delta OAB $$  cân tại O)

 $$ \Rightarrow \,\widehat{MOA}=\widehat{NOB} $$   $$ \Rightarrow \,\,\overset\frown{MA}=\overset\frown{NB} $$ .  (1)

Chứng minh tương tự ta có:  $$ \overset\frown{MC}=\overset\frown{ND} $$ . (2)

Vì điểm C nằm trên cung AM, điểm D nằm trên cung BN nên ta có:

sđ $$ \overset\frown{AC}= $$  sđ $$ \overset\frown{MA} $$  - sđ  $$ \overset\frown{MC} $$  ;  sđ $$ \overset\frown{BD}= $$  sđ $$ \overset\frown{BN} $$  - sđ  $$ \overset\frown{ND} $$ ;  (3)

Từ (1) (2) và (3) suy ra  $$ \overset\frown{AC}=\overset\frown{BD} $$ .

+ Trường hợp điểm O nằm trong hai dây song song (AB // CD)  (hình vẽ).

Chứng minh tương tự ta có:  $$ \,\,\overset\frown{MA}=\overset\frown{NB}\,\,; $$   $$ \overset\frown{MC}=\overset\frown{ND} $$ .

Vì điểm C nằm trên cung AM, điểm D nằm trên cung BN nên ta có:

sđ $$ \overset\frown{AC}= $$  sđ $$ \overset\frown{MA} $$  + sđ  $$ \overset\frown{MC} $$  ;  sđ $$ \overset\frown{BD}= $$  sđ $$ \overset\frown{BN} $$  + sđ $$ \overset\frown{ND} $$

Từ đó suy ra  $$ \overset\frown{AC}=\overset\frown{BD} $$ .

Vậy trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Bài 14 trang 72 SGK Toán 9 Tập 2

Bài 14 (trang 72 SGK Toán 9 tập 2): a) Chứng minh rằng đường kính đi qua hai điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.

Lời giải

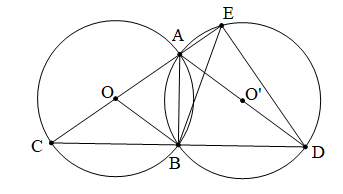
Lấy các điểm như hình vẽ.

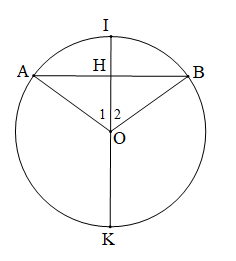
a) Điểm I là điểm chính giữa cung AB. Chứng minh H là trung điểm của AB

Vì điểm I là điểm chính giữa cung AB nên  $$ \overset\frown{AI}=\overset\frown{BI}\,\,\Rightarrow \,\,AI=BI. $$  

Mà  $$ OA=OB $$  (bán kính)

 $$ \Rightarrow  $$  IK là đường trung trực của AB  $$ \Rightarrow  $$   $$ HA=HB $$ .

Mệnh đề đảo: Đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung căng dây đó.

Chứng minh: Vì  $$ \Delta OAB $$  cân tại O và  $$ HA=HB $$  nên OH là đường phân giác của  $$ \widehat{AOB} $$    $$ \Rightarrow \,\,{{\widehat{O}}_{1}}={{\widehat{O}}_{2}} $$   $$ \Rightarrow \,\,\overset\frown{AI}=\overset\frown{BI} $$ .

Tuy nhiên điều này không thể xảy ra khi dây AB đi qua tâm O của đường tròn.

Vậy để mệnh đề đảo đúng thì cần thêm điều kiện: Dây AB không đi qua tâm O.

Vậy mệnh đề đảo phát biểu đúng là:

Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây đó.

b) Vì I là điểm chính giữa của cung AB nên  $$ \overset\frown{IA}=\overset\frown{IB}\,\,\Rightarrow \,\,IA=IB $$ .

Mà  $$ OA=OB $$  

Suy ra đường kính  $$ IK $$  là đường trung trực của dây  $$ AB $$  

Suy ra  $$ IK\bot AB $$  

* Điều ngược lại: Đường kính vuông góc ở dây khi qua tâm thì đi qua hai điểm chính giữa của cung căng dây đó.

Kẻ đường kính  $$ KOI $$  vuông góc với  $$ AB $$ .

Ta có  $$ OA=OB\,\,\Rightarrow \,\,\Delta OAB $$  cân tại O.

Mà  $$ OH\bot AB $$  nên OH là tia phân giác của  $$ \widehat{AOB} $$    $$ \Rightarrow \,\,{{\widehat{O}}_{1}}={{\widehat{O}}_{2}} $$

Ta có:  $$ \Delta OAI=\Delta OBI\,(c.g.c) $$ .

 $$ \Rightarrow \,\,AI=BI\,\,\Rightarrow \overset\frown{AI}=\overset\frown{BI} $$ .

Vậy I là điểm chính giữa của  $$ \overset\frown{AB} $$ .