Bài 27 trang 79 SGK Toán 9 Tập 2

Bài 27 (trang 79 SGK Toán 9 tập 2): Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh:

 $$ \widehat{APO}=\widehat{PBT} $$  

Lời giải

Ta có:  $$ \widehat{PAB} $$  là góc nội tiếp chắn cung PmB nên  $$ \,\,\widehat{PAB}=\frac{1}{2} $$  sđ $$ \overset\frown{PmB} $$ .  (1)

 $$ \widehat{PBT} $$  là góc tạo bởi tiếp tuyến BT và dây cung PB nên  $$ \,\,\widehat{PBT}=\frac{1}{2} $$  sđ $$ \overset\frown{PmB} $$ . (2)

Từ (1) và (2) suy ra  $$ \widehat{PAB}=\widehat{PBT} $$ .

Mà  $$ \widehat{PAB}=\widehat{APO} $$  (Do  $$ \Delta AOP $$  cân tại O)

 $$ \Rightarrow \,\widehat{APO}=\widehat{PBT} $$  (đpcm).

Bài 28 trang 79 SGK Toán 9 Tập 2

Bài 28 (trang 79 SGK Toán 9 tập 2): Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A cắt đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).

Lời giải

Nối A với B.

Xét đường tròn (O’) ta có: \[\widehat{AQB}\] là góc nội tiếp chắn cung  $$ \overset\frown{AmB} $$ ;  $$ \widehat{PAB} $$  là góc tạo bởi tiếp tuyến PA và dây cung AB

 $$ \Rightarrow \,\,\widehat{AQB}=\widehat{PAB} $$ ( $$ =\frac{1}{2} $$ sđ  $$ \overset\frown{AmB} $$ ).   (1)

Xét đường tròn (O) ta có:  $$ \widehat{PAB} $$  là góc nội tiếp chắn cung  $$ \overset\frown{PB} $$ ;  $$ \widehat{BPx} $$  là góc tạo bởi tiếp tuyến Px và dây cung PB

 $$ \Rightarrow \,\,\widehat{PAB}=\widehat{BPx} $$  (= $$ \frac{1}{2} $$  sđ  $$ \overset\frown{PB} $$ )  (2)

Từ (1) và (2) suy ra  $$ \widehat{AQB}=\widehat{BPx} $$ .

Mà hai góc này ở vị trí so le trong.

Do đó AQ // Px  (đpcm).

Bài 29 trang 79 SGK Toán 9 Tập 2

Bài 29 (trang 79 SGK Toán 9 tập 2): Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.

Chứng minh  $$ \widehat{CBA}=\widehat{DBA} $$ .

Lời giải

Xét đường tròn (O) ta có:  $$ \widehat{ACB} $$  là góc nội tiếp chắn cung AnB và  $$ \widehat{DAB} $$  là góc tạo bởi tiếp tuyến AD và dây cung AB  $$ \Rightarrow  $$   $$ \widehat{ACB}=\widehat{BAD} $$  ( $$ =\frac{1}{2} $$  sđ $$ \overset\frown{AnB} $$  ).

Xét đường tròn (O’) ta có:  $$ \widehat{ADB} $$  là góc nội tiếp chắn cung AmB và  $$ \widehat{CAB} $$  là góc tạo bởi tiếp tuyến AC và dây cung AB  $$ \Rightarrow \,\,\widehat{ADB}=\widehat{CAB} $$  (= $$ \frac{1}{2} $$  sđ $$ \overset\frown{AmB} $$ )  .

Xét  $$ \Delta ABC $$  và  $$ \Delta ABD $$  có:  $$ \widehat{ACB}=\widehat{BAD} $$  và  $$ \,\,\widehat{CAB}=\widehat{ADB} $$

 $$ \Rightarrow \,\,\,\,\widehat{CBA}=\widehat{DBA} $$  (đpcm).

Bài 30 trang 79 SGK Toán 9 Tập 2

Bài 30 (trang 79 SGK Toán 9 tập 2): Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn (h.29).

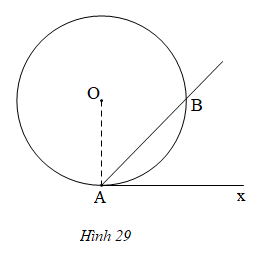
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.

Lời giải

Cách 1: Chứng minh trực tiếp.

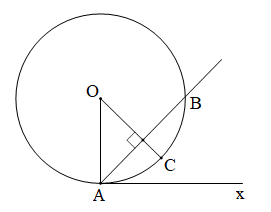
Kẻ bán kính OC vuông góc AB  $$ \Rightarrow  $$  C là điểm chính giữa  cung AB.

 $$ \Rightarrow \,\,\widehat{AOC}=\frac{1}{2} $$  sđ $$ \overset\frown{AC}=\frac{1}{2} $$  sđ $$ \overset\frown{AB} $$ .

Mà  $$ \widehat{BAx}=\frac{1}{2} $$  sđ $$ \overset\frown{AB} $$  (theo giả thiết)

 $$ \Rightarrow  $$    $$ \widehat{BAx}=\widehat{AOC} $$ .

Khi đó:  $$ \widehat{OAx}=\widehat{OAB}+\widehat{BAx}=\widehat{OAB}+\widehat{AOC}={{90}^{o}} $$  

 $$ \Rightarrow  $$  Ax là tiếp tuyến của đường tròn (O).

Cách 2: Chứng minh bằng phản chứng

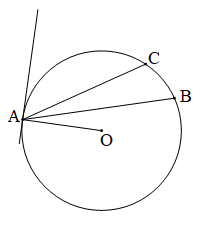
Nếu cạnh kia không phải là tiếp tuyến tại A mà là cát tuyến đi qua A và giả sử nó cắt đường tròn (O) tại C thì  $$ \widehat{BAC} $$  là góc nội tiếp  $$ \Rightarrow  $$    $$ \widehat{BAC}<\frac{1}{2} $$  sđ $$ \overset\frown{AB} $$  (Điều này trái với giả thiết ).

Vậy cạnh kia không phải là cát tuyến mà phải là tiếp tuyến Ax.

Bài 31 trang 79 SGK Toán 9 tập 2

Bài 31 (trang 79 SGK Toán 9 tập 2): Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính  $$ \widehat{ABC}\,,\,\widehat{BAC} $$ .

Lời giải

Xét tam giác BOC có  $$ OB=OC=BC=R $$  

 $$ \Rightarrow \,\,\Delta BOC $$  là tam giác đều  $$ \Rightarrow \,\,\widehat{BOC}={{60}^{o}} $$ .

Vì AB, AC là các tiếp tuyến của đường tròn (O) nên   $$ \widehat{ABC}=\widehat{ACB}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}{{.60}^{o}}={{30}^{o}} $$ ;

Xét tam giác ABC có  $$ \widehat{BAC}={{180}^{o}}-\left( \widehat{ABC}+\widehat{ACB} \right)={{180}^{o}}=\left( {{30}^{o}}+{{30}^{o}} \right)={{120}^{o}} $$ .

Bài 32 trang 80 SGK Toán 9 tập 2

Bài 32 (trang 80 SGK Toán 9 tập 2): Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T).

Chứng minh  $$ \widehat{BTP}+2\widehat{TPB}={{90}^{o}} $$ .

Lời giải

Ta có:  $$ \widehat{TPB} $$  là góc tạo bới tiếp tuyến PT và dây cung BP

 $$ \Rightarrow \,\,\widehat{TPB}=\frac{1}{2} $$  sđ $$ \overset\frown{BP} $$ .  (1)

 $$ \widehat{BOP} $$  là góc ở tâm chắn cung BP  $$ \Rightarrow \,\widehat{BOP}= $$  sđ $$ \overset\frown{BP} $$ .  (2)

Từ (1) và (2) suy ra  $$ \widehat{TPB}=\frac{1}{2}\widehat{POB} $$    $$ \Leftrightarrow \widehat{POB}=2\widehat{TPB} $$  (3)

Xét tam giác PTO có  $$ \widehat{TPO}={{90}^{o}} $$  (do PT là tiếp tuyến)

$$\Rightarrow \,\,\widehat{BTP}+\widehat{POB}={{90}^{o}}$$ $$\Rightarrow \,\,\widehat{PTB}+2\widehat{TPB}={{90}^{o}}$$ (do (3)).

Vậy   $$ \widehat{BTP}+2\widehat{TPB}={{90}^{o}} $$

Bài 33 trang 80 SGK Toán 9 tập 2

Bài 33 (trang 80 SGK Toán 9 tập 2): Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh AB.AM = AC.AN.

Lời giải

Ta có  $$ \widehat{tAB} $$  là góc tạo bởi tiếp tuyến At và dây cung AB,  $$ \widehat{ACB} $$  là góc nội tiếp chắn cung AB

 $$ \Rightarrow \,\widehat{tAB}=\widehat{ACB} $$ .

Mà  $$ \widehat{tAB}=\widehat{AMN} $$  (so le trong do At // MN)

 $$ \Rightarrow \,\,\widehat{ACB}=\widehat{AMN} $$ .

Xét  $$ \Delta AMN $$  và  $$ \Delta ACB $$  có  $$ \,\,\widehat{ACB}=\widehat{AMN} $$  ;  $$ \widehat{MAN} $$  chung

 $$ \Rightarrow  $$   $$ \Delta AMN $$  đồng dạng với  $$ \Delta ACB $$  (g.g)

 $$ \Rightarrow  $$   $$ \frac{AM}{AC}=\frac{AN}{AB}\,\,\Rightarrow \,\,AM.AB=AC.AN $$  (đpcm).

Bài 34 trang 80 SGK Toán 9 tập 2

Bài 34 (trang 80 SGK Toán 9 tập 2): Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.

Chứng minh \[M{{T}^{2}}=MA.MB.\]

Lời giải

Ta có:  $$ \widehat{MTA} $$  là góc tạo bởi tiếp tuyến MT và dây cung AT,  $$ \widehat{ABT} $$  là góc nội tiếp chắn cung AT

 $$ \Rightarrow \,\,\widehat{MTA}=\widehat{ABT} $$ . (1)

Xét   $$ \Delta MAT $$  và  $$ \Delta MTB $$  có:  $$ \widehat{M} $$  chung ;  $$ \widehat{MTA}=\widehat{MBT} $$ (do (1))

 $$ \Rightarrow  $$   $$ \Delta MAT $$ đồng dạng với  $$ MTB $$  (g,g)

 $$ \Rightarrow \,\,\frac{MA}{MT}=\frac{MT}{MB}\,\,\Rightarrow \,\,M{{T}^{2}}=MA.MB $$  (đpcm).

Bài 35 trang 80 SGK Toán 9 tập 2

Bài 35 (trang 80 SGK Toán 9 tập 2): Trên bờ biển có một ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trong thấy ngọn đèn này, biết rằng mắt người quan sát ở độ cao 10m so với mực nước biển và bán kính Trái Đất gần bằng 6400km (h.30)?

Lời giải

$$40m = 0,04km ; 10m = 0,01km$$

Áp dụng kết quả bài 34, ta có:

 $$ M{{T}^{2}}=MA.MB $$   $$ =MA.(MA+2R) $$

 $$ \Rightarrow \,M{{T}^{2}}=0,04.(0,04 + 2 . 6400)\,\,\Rightarrow \,\,MT\approx 23\,(km) $$ .

Tương tự ta có:

 $$ M'{{T}^{2}}=0,01.(0.01+ 2 . 6400)\,\approx 11\,(km). $$  

Do đó:  $$ MM'=MT+M'T\approx 23+11=34\,(km). $$   

Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.