Bài 42 trang 83 SGK Toán 9 tập 2
Bài 42 (trang 83 SGK Toán 9 tập 2): Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
a) Chứng minh AP ⊥ QR.
b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Lời giải
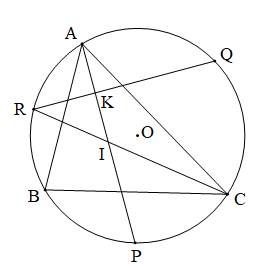
a) Gọi K là giao điểm của AP và QR.
$$ \widehat{AKR} $$ là góc có đỉnh ở bên trong đường tròn
$$ \Rightarrow $$ $$ \widehat{AKR}=\frac{1}{2} $$ (sđ $$ \overset\frown{AR}\,+ $$ sđ $$ \overset\frown{PQ} $$ ) $$ =\frac{1}{2} $$ (sđ $$ \overset\frown{AR}\,+ $$ sđ $$ \overset\frown{QC}+ $$ sđ $$ \overset\frown{PC} $$ )
$$ \Rightarrow \,\,\,\widehat{AKR} $$ $$ =\frac{1}{2}.\frac{1}{2} $$ (sđ $$ \overset\frown{AB}\,+ $$ sđ $$ \overset\frown{AC}+ $$ sđ $$ \overset\frown{BC} $$ ) $$ =\frac{1}{4}{{.360}^{o}}={{90}^{o}} $$
$$ \Rightarrow \,\,AP\bot QR $$ (đpcm).
b) $$ \widehat{CIP} $$ là góc có đỉnh ở bên trong đường tròn
$$ \Rightarrow $$ $$ \widehat{CIP}=\frac{1}{2} $$ (sđ $$ \overset\frown{AR}\,+ $$ sđ $$ \overset\frown{CP} $$ ) (1)
$$ \widehat{PCI} $$ là góc nội tiếp chắn cung PR $$ \Rightarrow \,\,\widehat{PCI}=\frac{1}{2} $$ sđ $$ \overset\frown{PR} $$ $$ =\frac{1}{2} $$ (sđ $$ \overset\frown{RB}+ $$ sđ $$ \overset\frown{BP} $$ ) (2)
Mà $$ \overset\frown{AR}=\overset\frown{RB} $$ ; $$ \overset\frown{CP}=\overset\frown{BP} $$ (3)
Từ (1) (2) và (3) suy ra $$ \widehat{CIP}=\widehat{PCI} $$ $$ \Rightarrow \,\,\Delta CPI $$ cân tại P (đpcm).