LÝ THUYẾT
1. Bài toán quỹ tích “cung chứa góc”
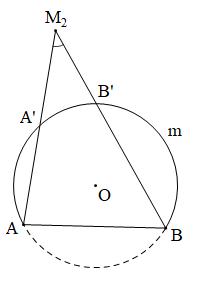
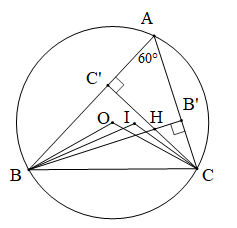
Với đoạn thẳng AB và góc $$ \alpha \,\,({{0}^{o}}<\alpha <{{180}^{o}}) $$ cho trước thì quỹ tích các điểm M thỏa mãn $$ \widehat{AMB}=\alpha $$ là hai cung chứa góc $$ \alpha $$ dựng trên đoạn AB.
- Chú ý
- Hai cung chứa góc $$ \alpha $$ nói trên là hai cung tròn đối xứng nhau qua AB,
- Hai điểm A, B được coi là thuộc quỹ tích.
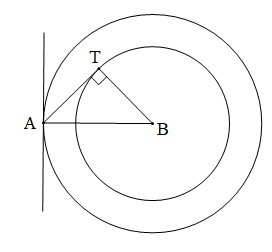
- Khi $$ \alpha ={{90}^{o}} $$ thì hai cung chứa góc $$ \alpha $$ đó là hai nửa đường tròn đường kính AB.
Như vậy: Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
2. Cách giải bài toán quỹ tích
Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:
Phần thuận: Mọi điểm của tính chất T đều thuộc hình H.
Phần đảo: Mọi điểm thuộc hình H đều có tính chất T.
Kết luận: Quỹ tích (hay tập hợp) các điểm có tính chất T là hình H.


.PNG)