LÝ THUYẾT
1. Khái ni·ªám
M·ªôt t·ª© giác có b·ªën ƒë·ªânh n·∫±m trên ƒë∆∞·ªùng tròn ƒë∆∞·ª£c g·ªçi là t·ª© giác n·ªôi ti·∫øp ƒë∆∞·ªùng tròn (g·ªçi t·∫Øt là t·ª© giác n·ªôi ti·∫øp).
2. ƒê·ªãnh lí
Trong m·ªôt t·ª© giác n·ªôi ti·∫øp, t·ªïng s·ªë ƒëo hai góc ƒë·ªëi nhau b·∫±ng $$ {{180}^{o}} $$ .
3. ƒê·ªãnh lí ƒë·∫£o
N·∫øu m·ªôt t·ª© giác có t·ªïng s·ªë ƒëo hai góc ƒë·ªëi nhau b·∫±ng $$ {{180}^{o}} $$ thì t·ª© giác ƒëó n·ªôi ti·∫øp ƒë∆∞·ª£c ƒë∆∞·ªùng tròn.
4. Các d·∫•u hi·ªáu nh·∫≠n bi·∫øt t·ª© giác n·ªôi ti·∫øp:
- T·ª© giác có t·ªïng hai góc ƒë·ªëi nhau b·∫±ng $$ {{180}^{o}} $$ .
- T·ª© giác có góc ngoài t·∫°i m·ªôt ƒë·ªânh b·∫±ng góc trong t·∫°i ƒë·ªânh ƒë·ªëi c·ªßa ƒë·ªânh ƒëó.
- T·ª© giác có b·ªën ƒë·ªânh cách ƒë·ªÅu m·ªôt ƒëi·ªÉm (mà ta có th·ªÉ xác ƒë·ªãnh ƒë∆∞·ª£c). ƒêi·ªÉm ƒëó là tâm c·ªßa ƒë∆∞·ªùng tròn ngo·∫°i ti·∫øp t·ª© giác.
- T·ª© giác có hai ƒë·ªânh k·ªÅ nhau cùng nhìn c·∫°nh ch·ª©a hai ƒë·ªânh còn l·∫°i d∆∞·ªõi m·ªôt góc $$ \alpha $$ .


.png)
.png)

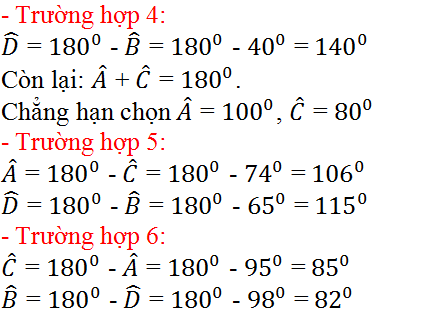
.PNG)
.png)