Bài 77 trang 98 SGK Toán 9 Tập 2

Bài 10: Diện tích hình tròn, hình quạt tròn

Bài 77 (trang 98 SGK Toán 9 tập 2): Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4cm.

Lời giải

Hình tròn nội tiếp hình vuông có cạnh 4cm thì có R = 2cm.

Vậy diện tích hình tròn là: π2² = 4π (cm²).

Bài 78 trang 98 SGK Toán 9 Tập 2

 Bài 78 (trang 98 SGK Toán 9 tập 2): Chân một đồng cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi 12m. Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông?

Lời giải

Theo giả thiết ta có:  $$ C=2\pi \,R\,\,\Rightarrow \,\,R=\frac{C}{2\pi }=\frac{12}{2\pi }=\frac{6}{\pi }\,(m). $$  

Diện tích phần mặt đất mà đống cát chiếm chỗ là:

 $$ S=\pi .{{R}^{2}}=\pi .{{\left( \frac{6}{\pi } \right)}^{2}}=\frac{36}{\pi }\approx 11,46\,({{m}^{2}}). $$  

Bài 79 trang 98 SGK Toán 9 Tập 2

Bài 79 (trang 98 SGK Toán 9 tập 2): Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là  $$ 36^o. $$

Lời giải

Diện tích hình quạt tròn là:  $$ S=\frac{\pi {{R}^{2}}.n}{360}=\frac{\pi {{.6}^{2}}.36}{360}=3,6\,\pi \,({{m}^{2}})\,. $$  

Bài 80 trang 98 SGK Toán 9 Tập 2

Bài 80 (trang 98 SGK Toán 9 tập 2): Một vườn cỏ hình chữ nhật ABCD có AB = 40m, AD = 30m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

- Mỗi dây thừng dài 20m.

- Một dây thừng dài 30m và dây thừng kia dài 10m.

Hỏi với cách buộc nào thì diện tích cỏ mà cả hai con dê có thể ăn được sẽ lớn hơn (h.60)?

Lời giải

- Theo cách buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.

Mỗi diện tích là  $$ \frac{1}{4} $$  diện tích hình tròn có bán kính 20m.

Vậy diện tích mà cả hai con dê ăn được theo cách buộc này là:  $$ 2.\frac{1}{4}\pi {{.20}^{2}}=200\pi \,({{m}^{2}}). $$  (1)

- Theo cách buộc thứ hai : Một dây thừng dài 30m và dây thừng kia dài 10m.

Diện tích cỏ dành cho cả hai  con dê là:  $$ \frac{1}{4}\pi {{.30}^{2}}+\frac{1}{4}\pi {{.10}^{2}}=250\,\pi \,\,({{m}^{2}}) $$ .  (2)

So sánh (1) và (2) ta thấy cách buộc thứ hai thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn.

Bài 81 trang 99 SGK Toán 9 Tập 2

Bài 81 (trang 99 SGK Toán 9 tập 2): Diện tích hình tròn sẽ thay đôi thế nào nếu:

a) Bán kính tăng gấp đôi?

b) Bán kính tăng gấp ba?

c) Bán kính tăng k lần (k > 1)?

Lời giải

Diện tích hình tròn lúc đầu là:  $$ S=\pi {{R}^{2}} $$ .

a) Khi bán kính tăng gấp đôi, tức là:  $$ {{R}_{1}}=2R $$ .

Ta có:  $$ {{S}_{1}}=\pi R_{1}^{2}=\pi .{{(2R)}^{2}}=4\pi {{R}^{2}}=4S. $$  

Vậy diện tích tăng gấp 4 lần khi bán kính tăng gấp đôi.

b) Khi bán kính tăng gấp ba, tức là:  $$ {{R}_{2}}=3R $$ .

Ta có:  $$ {{S}_{2}}=\pi R_{2}^{2}=\pi .{{(3R)}^{2}}=9\pi {{R}^{2}}=9S. $$  

Vậy diện tích tăng gấp 9 lần khi bán kính tăng gấp ba.

c) Khi bán kính tăng  $$ k $$  lần \[\left( k>1 \right)\], tức là:  $$ {{R}_{k}}=kR $$ .

Ta có:  $$ {{S}_{k}}=\pi R_{k}^{2}=\pi {{(kR)}^{2}}={{k}^{2}}\pi {{R}^{2}}={{k}^{2}}.S $$ .

Vậy diện tích tăng gấp  $$ {{k}^{2}} $$  lần khi bán kính tăng gấp  $$ k $$  lần.

Bài 82 trang 99 SGK Toán 9 Tập 2

Bài 10: Diện tích hình tròn, hình quạt tròn

Bài 82 (trang 99 SGK Toán 9 tập 2): Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất):

Lời giải

Áp dụng công thức

 $$ C=2\pi R\,\,\Rightarrow \,\,R=\frac{C}{2\pi }\,;\, $$  

 $$ S=\pi {{R}^{2}}\,\,\Rightarrow \,R=\sqrt{\frac{S}{\pi }} $$ ;

 _{$$ S $$ quạt}    $$ =\frac{\pi {{R}^{2}}n}{360} $$    .

Bài 83 trang 99 SGK Toán 9 tập 2

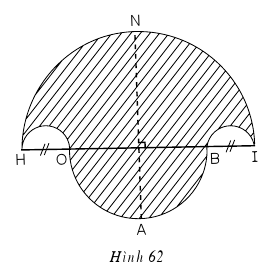
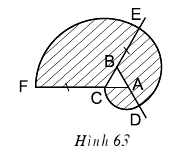
Bài 83 (trang 99 SGK Toán 9 tập 2): a) Vẽ hình 62 (tạo bởi các cung tròn) với $$ HI = 10cm$$ và $$HO = BI = 2cm.$$ Nêu cách vẽ.

b) Tính diện tích hình HOABINH (miền gạch sọc).

c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .

Lời giải

a) Cách vẽ

- Vẽ đoạn thẳng  $$ HI=10cm $$ . Trên HI vẽ điểm O và B sao cho  $$ HO=BI=2 $$ .

- Vẽ nửa đường tròn đường kính HI, tâm M.

- Vẽ hai nửa đường tròn đường kính HO và đường kính BI nằm cùng phía với đường tròn (M).

- Vẽ nửa đường tròn đường kính OB nằm khác phía với đường tròn (M).

- Qua M kẻ đường thẳng vuông góc với HI cắt đường tròn (M) tại N, cắt đường tròn đường kính OB tại điểm A.

b) Ta có:  $$ OB=HI-HO-BI=10-2-2=6\,(cm). $$  

 Diện tích miền gạch sọc là:

 $$ S=\frac{1}{2}\pi .{{\left( \frac{HI}{2} \right)}^{2}}+\frac{1}{2}\pi {{\left( \frac{OB}{2} \right)}^{2}}-\frac{1}{2}\pi {{\left( \frac{OH}{2} \right)}^{2}}-\frac{1}{2}\pi {{\left( \frac{BI}{2} \right)}^{2}} $$  

    $$ =\frac{1}{2}\pi {{.5}^{2}}+\frac{1}{2}\pi .{{\left( \frac{10-4}{2} \right)}^{2}}-\pi {{.1}^{2}}=16\pi \,\,(c{{m}^{2}}). $$  

c) Ta có:  $$ NA=\frac{10}{2}+\frac{6}{2}=5+3=8\,(cm). $$

Diện tích hình tròn đường kính NA là:  $$ S'=\pi .{{\left( \frac{NA}{2} \right)}^{2}}=16\pi \,(c{{m}^{2}}). $$  

Bài 84 trang 99 SGK Toán 9 tập 2

Bài 84 (trang 99 SGK Toán 9 tập 2): a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).

b) Tính diện tích miền gạch sọc.

Lời giải

a) Cách vẽ

- Vẽ tam giác đều ABC cạnh 1 cm.

- Vẽ  $$ \frac{1}{3} $$  đường tròn tâm A, bán kính 1cm, ta được cung CD.-

- Vẽ  $$ \frac{1}{3} $$  đường tròn tâm B, ban skinhs 2cm, ta được cung DE.

- Vẽ  $$ \frac{1}{3} $$  đường tròn tâm C, bán kính 3cm ta được cung EF.

b) Diện tích hình quạt CAD là:  $$ {{S}_{1}}=\frac{1}{3}\pi {{.1}^{2}}=\frac{1}{3}\pi \,\,(c{{m}^{2}}). $$  

Diện tích hình quạt DBE là:  $$ {{S}_{2}}=\frac{1}{3}\pi {{.2}^{2}}=\frac{4}{3}\pi \,(c{{m}^{2}}). $$  

Diện tích hình quạt ECF là;  $$ {{S}_{3}}=\frac{1}{3}\pi {{.3}^{2}}=3\pi \,(c{{m}^{2}}) $$  .

Vậy diện tích phần gạch sọc là:  $$ S={{S}_{1}}+{{S}_{2}}+{{S}_{3}}=\frac{1}{3}\pi +\frac{4}{3}\pi +3\pi =\frac{14}{3}\pi \,(c{{m}^{2}}). $$   

Bài 85 trang 100 SGK Toán 9 tập 2

Bài 85 (trang 100 SGK Toán 9 tập 2): Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm  $$ \widehat{AOB}={{60}^{o}} $$  và bán kính đường tròn là 5,1cm (h.64).

Lời giải

Xét  $$ \Delta AOB $$  có  $$ OA=OB\,;\,\,\widehat{AOB}={{60}^{o}}\,\,\Rightarrow \,\,\Delta AOB $$  là tam giác đều

 $$ \Rightarrow \,\,{{S}_{\Delta ABC}}=\frac{{{R}^{2}}\sqrt{3}}{4}=\frac{5,{{1}^{2}}\sqrt{3}}{4}\approx 11,26\,(c{{m}^{2}}). $$  

Diện tích hình quạt tròn OAmB là:

 $$ {{S}_{OAmB}}=\frac{\pi {{R}^{2}}.n}{360}=\frac{\pi .5,{{1}^{2}}.60}{360}\approx 13,62\,(c{{m}^{2}}) $$ .

Diện tích viên phân AmB là:  $$ S={{S}_{OAmB}}-{{S}_{AOB}}\approx 13,62-11,26=2,36\,(c{{m}^{2}}). $$  

Bài 86 trang 100 SGK Toán 9 tập 2

Bài 86 (trang 100 SGK Toán 9 tập 2): Hình vành khăn là phần hình tròn giữa hai đường tròn đồng tâm (h.65).

a) Tính diện tích S của hình vành khăn theo \[{{R}_{1}}\] và \[{{R}_{2}}\] (giả sử \[{{R}_{1}}>{{R}_{2}}\]).

b) Tính diện tích hình vành khăn khi \[{{R}_{1}}=10,5cm\,,{{R}_{2}}=7,8cm.\]

Lời giải

a) Diện tích hình tròn  $$ (O\,;\,{{R}_{1}}) $$  là:  $$ {{S}_{1}}=\pi R_{1}^{2} $$ .

Diện tích hình tròn  $$ (O\,;\,{{R}_{1}}) $$  là:  $$ {{S}_{2}}=\pi R_{2}^{2} $$ .

Diện tích vành khăn là:  $$ S={{S}_{1}}-{{S}_{2}}=\pi \left( R_{1}^{2}-R_{2}^{2} \right). $$  

b) Thay \[{{R}_{1}}=10,5cm\,,{{R}_{2}}=7,8cm\] ta được:

 $$ S=\pi .(10,5-7,8)=2,7\pi \,\,(c{{m}^{2}}). $$  

Bài 87 trang 100 SGK Toán 9 tập 2

Bài 87 (trang 100 SGK Toán 9 tập 2): Lấy cạnh BC của một tam giác đều làm đường kính, vẽ môt nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy tính diện tích của hai hình viên phân được tạo thành.

Lời giải

Gọi nửa đường tròn tâm O đường kính BC cắt hai cạnh AB và AC lần lượt tại M và N.

Xét  $$ \Delta ONC $$  có  $$ OC=ON,\,\,\widehat{C}={{60}^{o}} $$  

 $$ \Rightarrow \,\,\Delta ONC $$  là tam giác đều  $$ \Rightarrow \,\,\widehat{NOC}={{60}^{o}} $$ .

Diện tích hình quạt NOC là:  $$ {{S}_{1}}=\frac{\pi .{{\left( \frac{a}{2} \right)}^{2}}.60}{360}=\frac{\pi {{a}^{2}}}{24}\,\,;\, $$  

Diện tích tam giác NOC là:  $$ {{S}_{2}}=\frac{{{\left( \frac{a}{2} \right)}^{2}}\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{16}. $$  

Diện tích một hình viên phân là:

 $$ {{S}_{CpN}}={{S}_{1}}-{{S}_{2}}=\frac{\pi {{a}^{2}}}{24}-\frac{{{a}^{2}}\sqrt{3}}{16}=\frac{{{a}^{2}}}{48}\left( 2\pi -3\sqrt{3} \right) $$ .

Diện tích của hai hình viên phân được tạo thành là:                               

 $$ S=2.{{S}_{CpN}}=2.\frac{{{a}^{2}}}{48}\left( 2\pi -3\sqrt{3} \right)=\frac{{{a}^{2}}}{24}\left( 2\pi -3\sqrt{3} \right) $$ .