LÝ THUYẾT
A. Các định nghĩa
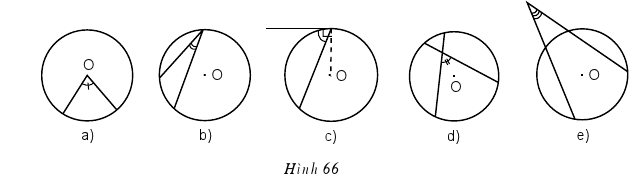
1. Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
2. Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
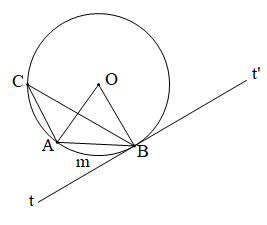
3. Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tia tiếp tuyến và cạnh kia chứa dây cung.
4. Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn.
5. Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.
6. Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.
B. Các định lí
1. Nếu C là một điểm nằm trên cung AB thì: sđ $$ \overset\frown{AB} $$ = sđ $$ \overset\frown{AC} $$ + sđ $$ \overset\frown{CB} $$ .
2. Với hai cung nhỏ trong một đường tròn, hai cung bằng nhau căng hai dây bằng nhau và ngược lại.
3. Với hai cung nhỏ của một đường tròn, cung lớn hơn căng dây lớn hơn và ngược lại.
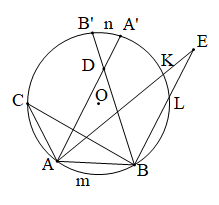
4. Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
5. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
6. Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cung chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp (nhỏ hơn hoặc bằng $$ {{90}^{o}} $$ ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn nửa đường tròn là góc vuông và ngược lại, góc vuông nội tiếp thì chắn nửa đường tròn.
- Góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
7. Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
8. Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
9. Quỹ tích (tập hợp) các điểm nhìn một đoạn thẳng cho trước dưới một góc $$ \alpha $$ không đổi là hai cung chứa góc $$ \alpha \, $$ dựng trên đoạn thẳng đó $$ ({{0}^{o}}<\alpha <{{180}^{o}}) $$ .
10. Một tứ giác có tổng hai góc đối nhau bằng $$ {{180}^{o}} $$ thì nội tiếp được đường tròn và ngược lại.
11. Dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có tổng hai góc đối nhau bằng $$ {{180}^{o}} $$ .
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc $$ \alpha $$ .
12. Hình thang nội tiếp được đường tròn là hình thang cân và ngược lại.
13. Bất kì một đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
14. Trên đường tròn bán kính R, độ dài $$ \ell $$ của một cung $$ {{n}^{o}} $$ được tính theo công thức
$$ \ell =\frac{\pi Rn}{180} $$ .
15. Diện tích S của hình quạt tròn bán kính R, cung $$ {{n}^{o}} $$ được tính theo công thức:
$$ S=\frac{\pi {{R}^{2}}n}{360} $$ hay $$ S=\frac{\ell R}{2} $$
( $$ \ell $$ là độ dài cung $$ {{n}^{o}} $$ của hình quạt tròn).