Bài 37 trang 126 SGK Toán 9 tập 2
Bài 37 (trang 126 SGK Toán 9 tập 2): Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh $$ AM.BN={{R}^{2}}. $$
c) Tính tỉ số $$ \frac{{{S}_{MON}}}{{{S}_{APB}}} $$ khi $$ AM=\frac{R}{2}. $$
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Lời giải
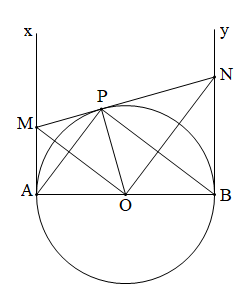
a) Ta có OM, ON lần lượt là tia phân giác của $$ \widehat{AOP}\,,\widehat{BOP} $$ (tính chất của hai tiếp tuyến cắt nhau).
Mà $$ \widehat{AOP} $$ kề bù với $$ \widehat{BOP} $$ nên suy ra OM vuông góc với ON.
Vậy \[\Delta MON\] vuông tại O.
Xét đường tròn (O) có $$ \widehat{APB} $$ là góc nội tiếp chắn nửa đường tròn nên $$ \widehat{APB}={{90}^{o}} $$
$$ \Rightarrow \,\Delta APB $$ vuông tại P.
Xét tứ giác AOPM có: $$ \widehat{MAO}=\widehat{MPO}={{90}^{o}} $$ $$ \Rightarrow $$ Tứ giác AOMP là tứ giác nội tiếp
$$ \Rightarrow \,\widehat{PMO}=\widehat{PAO} $$ (hai góc nội tiếp cùng chắn cung OP) (1)
Xét $$ \Delta MON $$ và $$ \Delta APB $$ có:
$$ \widehat{MON}=\widehat{APB}={{90}^{o}}\,;\,\,\widehat{OMN}=\widehat{BAP} $$ (do (1))
$$ \Rightarrow \,\,\Delta MON $$ đồng dạng với $$ \Delta APB $$ (g.g).
b) Xét $$ \Delta MON $$ vuông tại O có $$ OP\bot MN $$ nên áp dụng hệ thức lượng trong tam giác vuông ta có:
$$ O{{P}^{2}}=MP.PN $$ .
Mà $$ MP=MA\,;\,NP\,=\,NB $$ (tính chất tiếp tuyến cắt nhau).
$$ \Rightarrow \,\,O{{P}^{2}}=MA.NB $$ $$ \Rightarrow \,\,MA.NB={{R}^{2}} $$ .
c) Vì $$ \,\Delta MON $$ đồng dạng với $$ \Delta APB $$ nên $$ \frac{{{S}_{MON}}}{{{S}_{APB}}}={{\left( \frac{MN}{AB} \right)}^{2}} $$ .
Khi $$ AM=\frac{R}{2} $$ mà $$ AM.NB={{R}^{2}} $$ nên $$ NB=\frac{{{R}^{2}}}{AM}=\frac{{{R}^{2}}}{\frac{R}{2}}=2R $$ .
Ta có: $$ MN=MP+PN=AM+BN=\frac{R}{2}+2R=\frac{5R}{2} $$ .
Khi đó: $$ \frac{{{S}_{MON}}}{{{S}_{APB}}}={{\left( \frac{MN}{AB} \right)}^{2}}={{\left( \frac{\frac{5R}{2}}{2R} \right)}^{2}}=\frac{25}{16} $$ .
d) Nửa đường tròn APB quay quanh AB sinh ra một hình cầu có bán kính R.
Vậy thể tích của hình cầu đó là: $$ V=\frac{4}{3}\pi {{R}^{3}}. $$
.PNG)