Bài 30 trang 59 Toán 9 Tập 1
Bài 30 (trang 59 SGK Toán 9 Tập 1):
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
$$ y=\frac{1}{2}\,x+2 $$ ; $$ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y=-x+2 $$ .
b) Gọi giao điểm của hai đường thẳng $$ y=\frac{1}{2}\,x+2 $$ và $$ y=-x+2 $$ với trục hoành theo thứ tự là \[A,B\] và gọi giao điểm của hai đường thẳng đó là $$ C $$ . Tính các góc của tam giác \[ABC\] (làm tròn đến độ)
c) Tính chu vi và diện tích của tam giác \[ABC\] (đơn vị đo trên các trục tọa độ là xentimet).
Lời giải:
a)
- Vẽ đồ thị hàm số $$ y=\frac{1}{2}\,x+2 $$ .
Cho $$ y=0\Rightarrow \,\,\frac{1}{2}\,x+2=0\Leftrightarrow x=-4 $$ ta được $$ A\left( -4;0 \right) $$ .
Cho $$ x=0\,\,\Rightarrow y=\frac{1}{2}.0+2=2 $$ ta được $$ C(0;2) $$ .
Vậy đồ thị hàm số $$ y=\frac{1}{2}\,x+2 $$ là đường thẳng đi qua hai điểm $$ A\left( -4;0 \right) $$ và $$ C(0;2) $$ .
- Vẽ đồ thị hàm số \[y=-x+2\].
Cho \[x=0\Rightarrow y=2\] được \[C\left( 0;2 \right)\].
Cho \[y=0\,\,\Rightarrow x=2\] được \[B\left( 2;0 \right)\].
Vậy đồ thị hàm số \[y=-x+2\] là đường thẳng đi qua hai điểm \[B\left( 2;0 \right)\] và \[C\left( 0;2 \right)\].
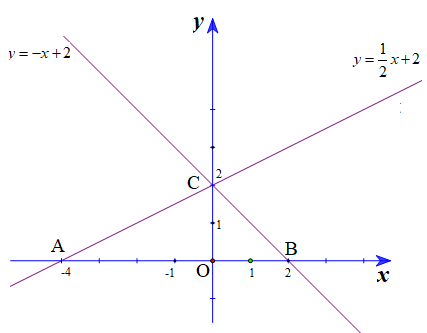
b) Tam giác $$ OBC $$ vuông cân tại O nên $$ \widehat{OBC}=\widehat{OCB}={{45}^{o}} $$ .
Xét tam giác $$ OAC $$ vuông tại O, ta có: $$ \tan \widehat{OAC}=\frac{OC}{OA}=\frac{2}{4}=\frac{1}{2}\, $$ $$ \Rightarrow \,\,\widehat{OAC}\,\approx {{27}^{o}} $$ .
Xét tam giác $$ ABC $$ có $$ \widehat{ACB}={{180}^{o}}-\left( \widehat{CAB}+\widehat{ABC} \right)\approx {{180}^{o}}-({{27}^{o}}+{{45}^{o}})={{108}^{o}} $$ .
c) Ta có: $$ OC=2\,cm\,;\,\,OA=4cm\,;\,OB=2cm $$ ; $$ AB=OA+OB=6cm. $$
Áp dụng định lí Pytago ta có:
$$ AC=\sqrt{O{{C}^{2}}+O{{A}^{2}}}=\sqrt{{{2}^{2}}+{{4}^{2}}}=\sqrt{20}=2\sqrt{5}\,(cm). $$
$$ BC=\sqrt{O{{B}^{2}}+O{{C}^{2}}}=\sqrt{{{2}^{2}}+{{2}^{2}}}=\sqrt{8}=2\sqrt{2}\,(cm). $$
Vậy chu vi tam giác $$ ABC $$ là: $$ AB+AC+BC=6+2\sqrt{5}+2\sqrt{2}\,(cm). $$
Diện tích tam giác $$ ABC $$ là: $$ {{S}_{ABC}}=\frac{1}{2}OC.AB=\frac{1}{2}.2.6=6\,(c{{m}^{2}}). $$
.png)