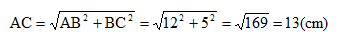LÝ THUYẾT
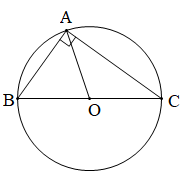
1. Định nghĩa: Đường tròn tâm O bán kính R (với R > 0) là hình gồm các điểm cách điểm O một khoảng bằng R.
Kí hiệu (O ; R).
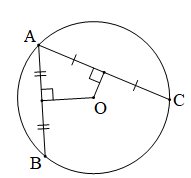
- Điểm M nằm trên đường tròn (O ; R) khi và chỉ khi OM = R.
- Điểm M nằm bên trong (hay nằm trong, ở trong) đường tròn (O ; R) khi và chỉ khi OM < R.
- Điểm M nằm bên ngoài (hay nằm ngoài, ở ngoài) đường tròn (O ; R) khi và chỉ khi OM > R.
2. Cách xác định đường tròn:
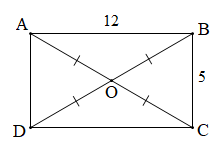
- Một đường tròn được xác định khi biết tâm và bán kính của đường tròn đó, hoặc khi biết một đoạn thẳng là đường kính của đường tròn đó.
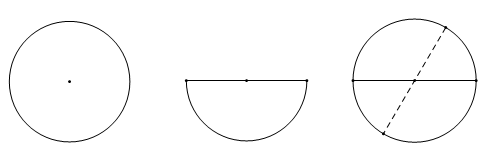
- Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
- Chú ý: Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng.
3. Tâm đối xứng và trục đối xứng:
- Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
- Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.