LÝ THUYẾT
1. Khái niệm phương trình bậc nhất hai ẩn.
- Phương trình bậc nhất hai ẩn $$x$$ và $$y$$ là hệ thức có dạng: \[ax+by=c,\] (1)
trong đó $$a, b$$ và $$c$$ là các số đã biết ( $$ a\ne 0 $$ hoặc $$ b\ne 0 $$ ).
- Trong phương trình (1) nếu giá trị của vế trái tại $$ x={{x}_{0}} $$ và $$ y={{y}_{0}} $$ bằng vế phải thì cặp số $$ ({{x}_{0}}\,;\,{{y}_{0}}) $$ được gọi là một nghiệm của phương trình (1).
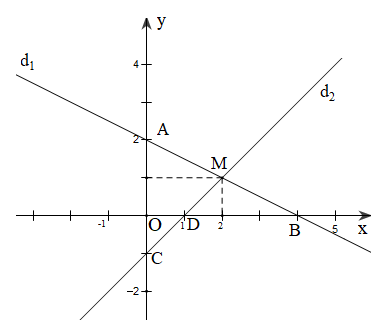
- Trong mặt phẳng tọa độ $$Oxy,$$ nghiệm $$ ({{x}_{0}};{{y}_{0}}) $$ được biểu diễn bởi điểm có tọa độ $$ ({{x}_{0}};{{y}_{0}}). $$
2. Tập nghiệm của phương trình bậc nhất hai ẩn.
- Phương trình bậc nhất hai ẩn \[ax+by=c\] luôn luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng \[ax+by=c,\] kí hiệu là (d).
- Nếu $$ a\ne 0 $$ và $$ b\ne 0 $$ thì đường thẳng (d) chính là đồ thị của hàm số bậc nhất: $$ y=-\frac{a}{b}x+\frac{c}{d}. $$
- Nếu $$ a\ne 0 $$ và $$ b=0 $$ thì phương trình trở thành $$ ax=c $$ hay $$ x=\frac{c}{a} $$ , và đường thẳng (d) song song hoặc trùng với trục tung.
- Nếu $$ a=0 $$ và $$ b\ne 0 $$ thì phương trình trở thành $$ by=c $$ hay $$ y=\frac{c}{b}, $$ và đường thẳng (d) song song hoặc trùng với trục hoành.



.PNG)
.PNG)

.PNG)
.PNG)