LÝ THUYẾT
1. Đồ thị của hàm số $$ y=ax+b\,\,(\,a\ne 0) $$ :
Đồ thị của hàm số $$ y=ax+b\,\,(\,a\ne 0) $$ là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng $$b;$$
- Song song với đường thẳng $$y = ax,$$ nếu $$ b\ne 0 $$ ; trùng với đường thẳng $$y = ax$$, nếu $$b = 0.$$
- Chú ý: Đồ thị của hàm số $$ y=ax+b\,\,(\,a\ne 0) $$ còn được gọi là đường thẳng $$ y=ax+b $$ ; b được gọi là tung độ gốc của đường thẳng.
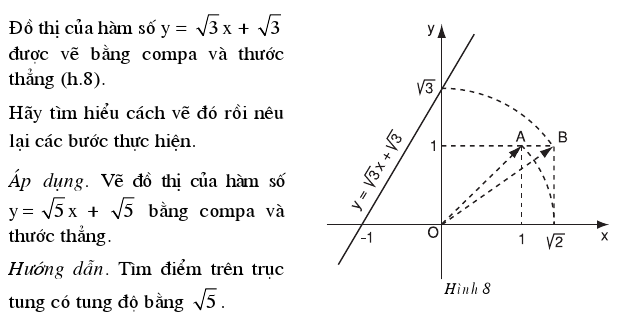
2. Cách vẽ đồ thị của hàm số $$ y=ax+b\,\,(\,a\ne 0) $$ :
- Khi $$b = 0$$ thì $$y = ax.$$ Đồ thị của hàm số $$y = ax $$ là đường thẳng đi qua gốc tọa độ $$O(0 ; 0)$$ và điểm $$A(1 ; a).$$
- Xét trường hợp $$ y = ax + b$$ với $$ a\ne 0 $$ và $$ b\ne 0 $$ .
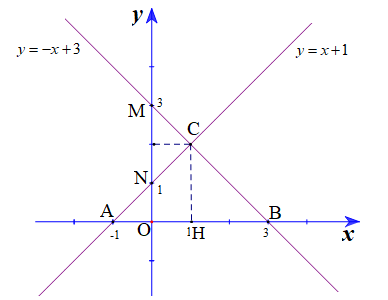
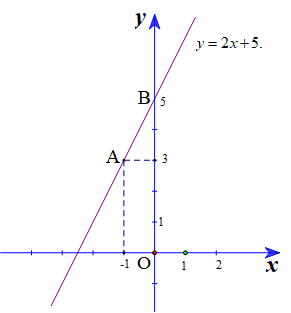
- Bước 1: Cho $$x = 0$$ thì $$y = b,$$ ta được điểm $$A(0 ; b)$$ thuộc trục tung $$Oy.$$
Cho $$y = 0$$ thì $$ x=-\frac{b}{a} $$ ta được điểm $$ B\left( -\frac{b}{a}\,;\,0 \right) $$ thuộc trục hoành $$Ox.$$
- Bước 2: Vẽ đường thẳng đi qua hai điểm $$A $$ và $$B$$ ta được đồ thị của hàm số $$ y=ax+b $$ .



.png)
.png)


.png)
.png)
.png)



