Bài 27 trang 88 Toán 9 Tập 1
Bài 27 (trang 84 SGK Toán 9 Tập 1): Giải tam giác ABC vuông tại A, biết rằng
a) $$ b=10cm,\,\,\widehat{C}={{30}^{o}}\,; $$
b) $$ c=10m,\,\,\widehat{C}={{45}^{o}} $$ .
c) $$ a=20cm,\,\,\widehat{B}={{35}^{o}} $$ .
d) $$ c=21cm,\,\,b=18cm. $$
Lời giải:
a)
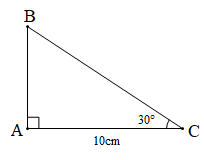
$$ \Delta ABC $$ vuông tại A nên $$ \widehat{B}+\widehat{C}={{90}^{o}}\Leftrightarrow \widehat{B}={{90}^{o}}-\widehat{C}={{90}^{o}}-{{30}^{o}}={{60}^{o}}. $$
$$ c=AB=AC.tgC=10.tg{{30}^{o}}=\frac{10\sqrt{3}}{3}\,(cm). $$
$$ a=\frac{b}{\sin B}=\frac{10}{\sin {{60}^{o}}}=\frac{10\sqrt{3}}{3}\,(cm). $$
b)
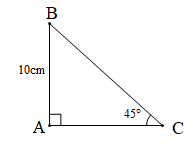
$$ \Delta ABC $$ vuông tại A có $$ \widehat{C}={{45}^{o}} $$ nên $$ \Delta ABC $$ vuông cân tại A
$$ \Rightarrow \,\,\widehat{B}=\widehat{C}={{45}^{o}}\,;\,b=c=10cm. $$
$$ a=\frac{b}{\sin B}=\frac{10}{\sin {{45}^{o}}}=10\sqrt{2}\,(cm). $$
c)
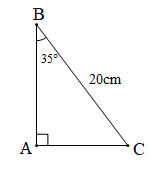
$$ \widehat{B}={{90}^{o}}-\widehat{C}={{90}^{o}}-{{35}^{o}}={{55}^{o}}. $$
$$ b=AC=BC.\sin B=20\sin {{35}^{o}}\approx 11,47\,\,(cm) $$ .
$$ c=AB=BC\sin C=20\sin {{55}^{o}}\approx 16,38\,(cm). $$
d)
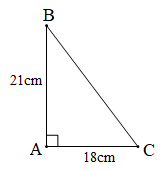
$$ tgB=\frac{AC}{AB}=\frac{18}{21}\,\,\Rightarrow \,\widehat{B}\approx {{41}^{o}}. $$
$$ \widehat{C}={{90}^{o}}-\widehat{B}\,\approx {{90}^{o}}-{{41}^{o}}={{49}^{o}}. $$
$$ a=BC=\frac{AC}{\sin B}=\frac{18}{\sin {{41}^{o}}}\approx 27,44\,(cm). $$
(Ghi chú: Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))




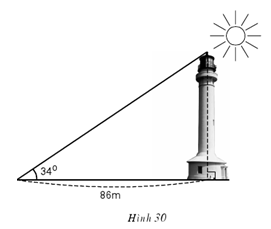
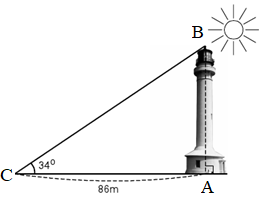




.png)
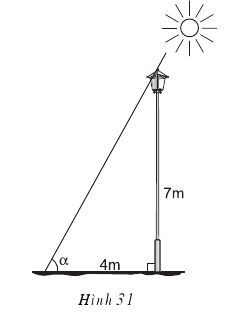
.png)
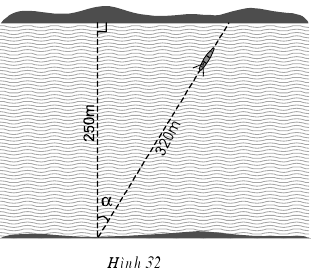
.PNG)



