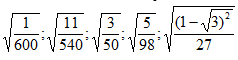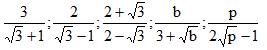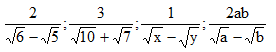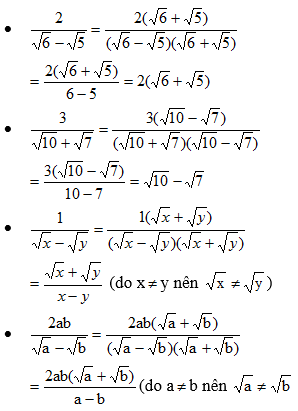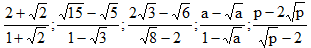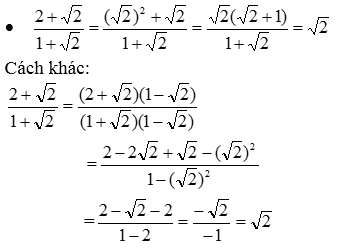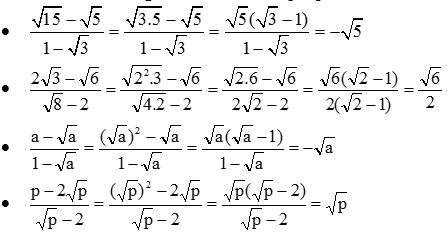LÝ THUYẾT
1. Khử mẫu của biểu thức lấy căn:
Với các biểu thức \[A,\,B\] mà $$ A.B\ge 0 $$ và $$ B\ne 0 $$ , ta có: $$ \sqrt{\frac{A}{B}}=\frac{\sqrt{AB}}{|B|} $$ .
2. Trục căn thức ở mẫu:
- Với các biểu thức \[A,B\] mà \[B>0\], ta có: $$ \frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B} $$ .
- Với các biểu thức \[A,B,C\] mà $$ A\ge 0 $$ và $$ A\ne {{B}^{2}} $$ , ta có:
$$ \frac{C}{\sqrt{A}+B}=\frac{C\left( \sqrt{A}-B \right)}{A-{{B}^{2}}}\,\,;\,\,\,\,\,\frac{C}{\sqrt{A}-B}=\frac{C\left( \sqrt{A}+B \right)}{A-{{B}^{2}}} $$ .
- Với các biểu thức \[A,B,C\] mà $$ A\ge 0,\,B\ge 0 $$ và $$ A\ne B $$ , ta có:
$$ \frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left( \sqrt{A}-\sqrt{B} \right)}{A-B}\,\,;\,\,\,\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left( \sqrt{A}+\sqrt{B} \right)}{A-B} $$ .