Lý thuyết chương III: Khối đa diện - Khối tròn xoay - Phương pháp tọa độ trong không gian

Số trang: 47
Lượt đọc: 6521
Lượt tải: 77
Tác giả: HOCMAI
15:40 15/01/2019

I. Khối đa diện là gì?

1. Khái niệm hình đa diện

Để có thể hiểu rõ về khái niệm khối đa diện, chúng ta cần hiểu rõ về khái niệm hình đa diện. Hình đa diện là hình có cấu tạo từ một số hữu hạn các đa giác và phải thỏa mãn một số tính chất sau.

a) Hai đa giác phân biệt chỉ có thể có một trong những tính chất sau:

+ Không có điểm chung với nhau

+ Chỉ có một cạnh chung hoặc chỉ có 1 đỉnh chung

b) Mỗi cạnh của một đa giác bất kỳ trong hình đa diện phải là cạnh chung của chỉ 2 đa giác

Khi thỏa mãn các điều kiện trên thì mỗi đa giác trên là một mặt của hình đa diện. Các cạnh và đỉnh của các đa giác này tương ứng là cạnh và đỉnh của hình đa diện.

2. Khái niệm khối đa diện

Khối đa diện là toàn bộ phần không gian được giới hạn bởi hình đa diện (bao gồm cả bề mặt của hình đa diện đó).

Tập hợp những điểm nằm trong khối đa diện (không nằm trên bề mặt) được gọi là miền trong của khối đa diện. Và ngược lại, tập hợp những điểm nằm ngoài khối đa diện được gọi là miền ngoài của khối đa diện.

II. Các loại khối đa diện

Các khối đa diện rất đa dạng về hình dáng, tuy nhiên thông thường ta chia khối đa diện làm 2 loại chính:

- Khối đa diện lồi: Một khối đa diện (H) là khối đa diện lồi nếu đoạn thẳng được nối từ 2 đỉnh bất kỳ của của đa diện (H) luôn thuộc (H). Ngoài ra, một khác niệm khác về khối đa diện lồi: một đa diện lồi khi và chỉ khi miền trong của khối đa diện đó luôn nằm về một phía đối với bất kỳ mặt phẳng nào đi qua một mặt của khối đa diện đó.

- Khối đa diện lõm: các khối đa diện không thỏa mãn những điều kiện trên.

Đặc biệt:

Một khối đa diện có tất cả các mặt của khối đa diện đó là các đa giác đều, bằng nhau thì khối đa diện đó được gọi là khối đa diện đều.

Các bạn có thể tham khảo hoặc đăng ký: Học toán lớp 12 online miễn phí

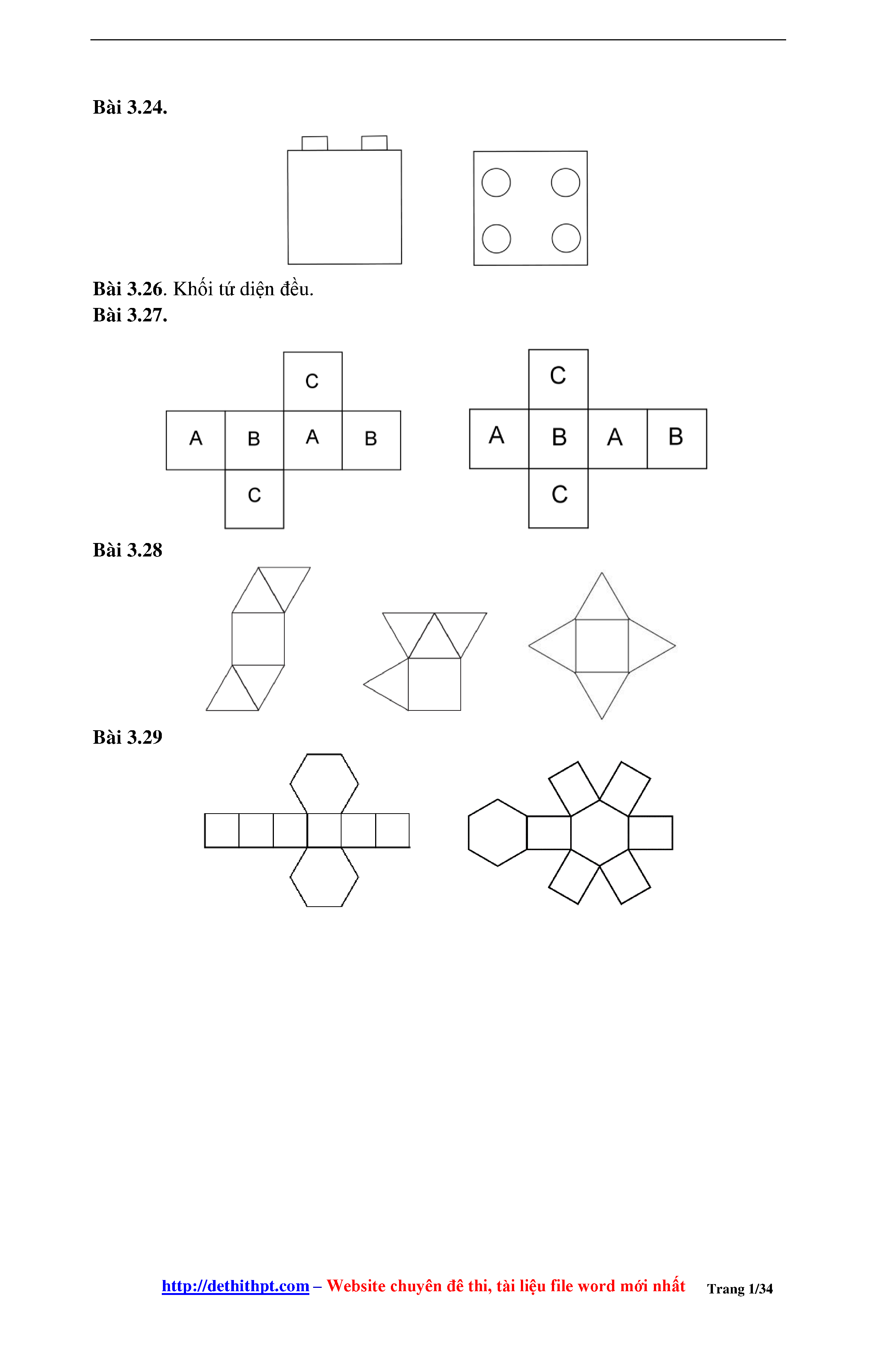
III. Phân chia và lắp ghép các khối đa diện

Những hình ảnh đời thường một khối phô mai bị cắt, những mẩu xếp hình được lắp ghép lại với nhau là những ví dụ sinh động và trực quan nhất cho việc phân chia và lắp ghép các khối trong không gian.

1. Nguyên tắc phân chia và lắp ghép các khối đa diện

Việc lắp ghép cũng như phân chia các khối đa diện cũng cần tuân thủ một số nguyên tắc nhất định.

Ví dụ đối với một khối đa diện đều là hình lập phương, ta có thể cắt khối này theo nhiều phương pháp khác nhau. Tương ứng với mỗi cách cắt, ta tạo được một số khối đa diện mới (ta tạm gọi đây là các khối thành phần - là các thành phần nhỏ của khối lập phương ban đầu). Những khối thành phần tạo ra từ một cách cắt sẽ lắp ghép được lại với nhau để trở thành khối lập phương ban đầu. (Các bạn có thể xem hình 3.2.2.a Slide số 3).

Tuy nhiên nếu lấy các khối thành phần từ những cách cắt khác nhau để lắp ghép thì chưa chắ sẽ trở thành khối lập phương ban đầu. (Các bạn có thể xem hình 3.2.2.b và 3.2.2.c Slide số 3).

Như vậy, ta có thể thấy được nguyên tắc phân chia và lắp ghép các khối đa diện được diễn tả như sau:

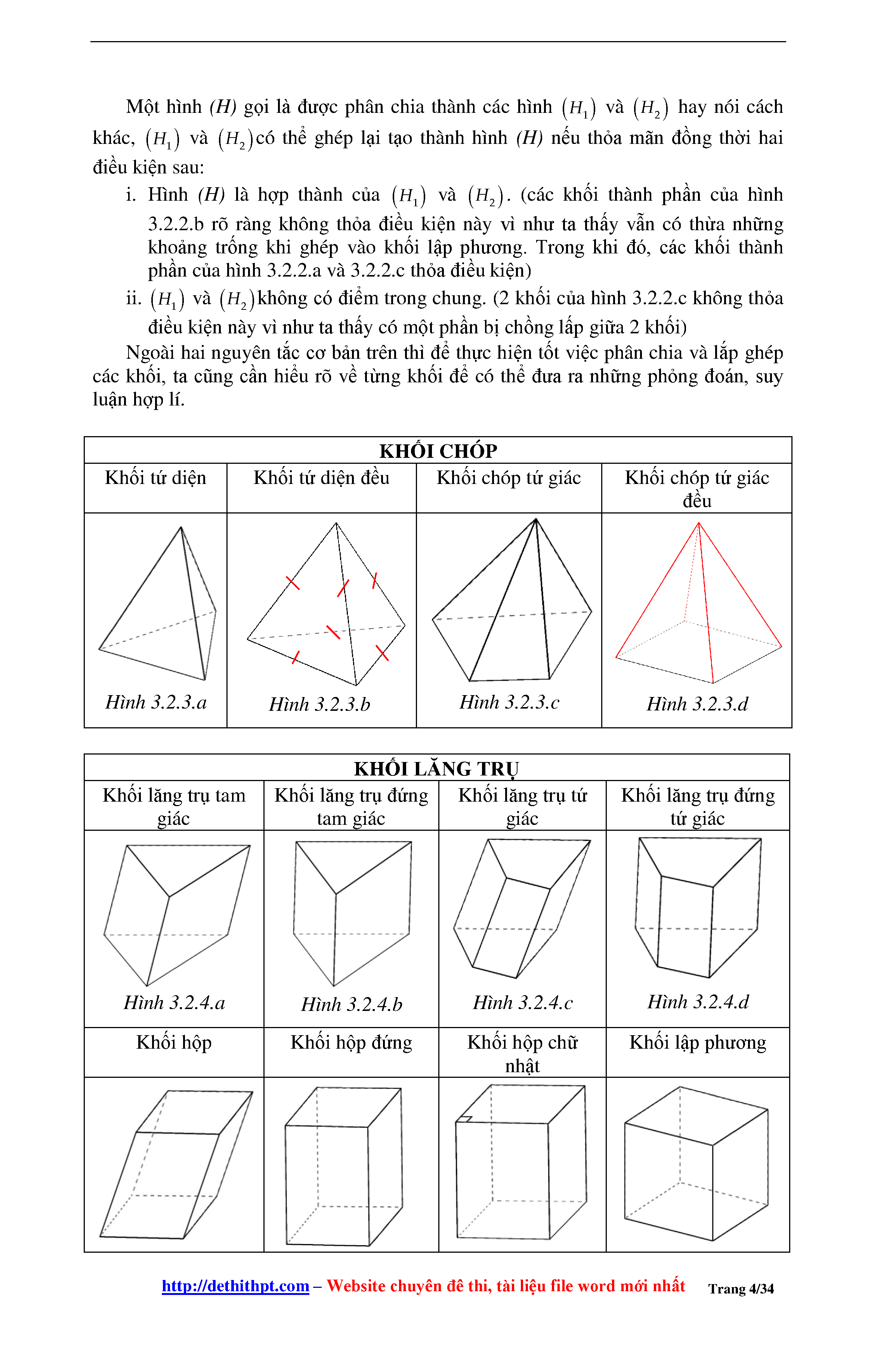
Một hình (H) gọi là được phân chia thành các hình (H1) và (H2) hay (H1) và (H2) có thể ghép lại tạo thành hình (H) khi thỏa mãn đồng thời 2 điều kiện dưới đây:

- Hình (H) là hợp thành của (H1) và (H2)

- Hình (H1) và (H2) không có điểm trong chung.

Tham khảo ngay khóa học: ôn thi đại học môn toán để nhận được rất nhiều ưu đãi hấp dẫn

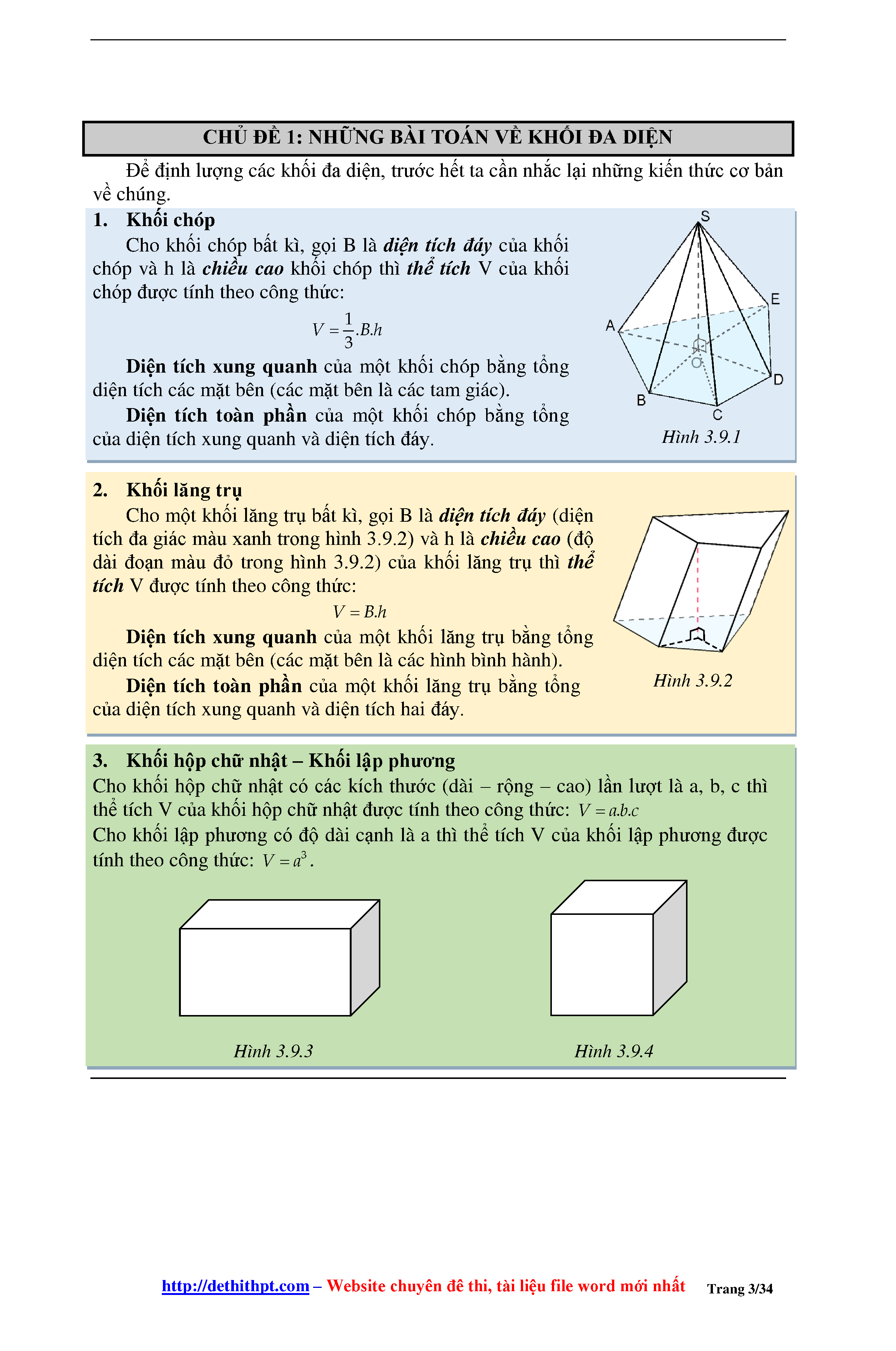
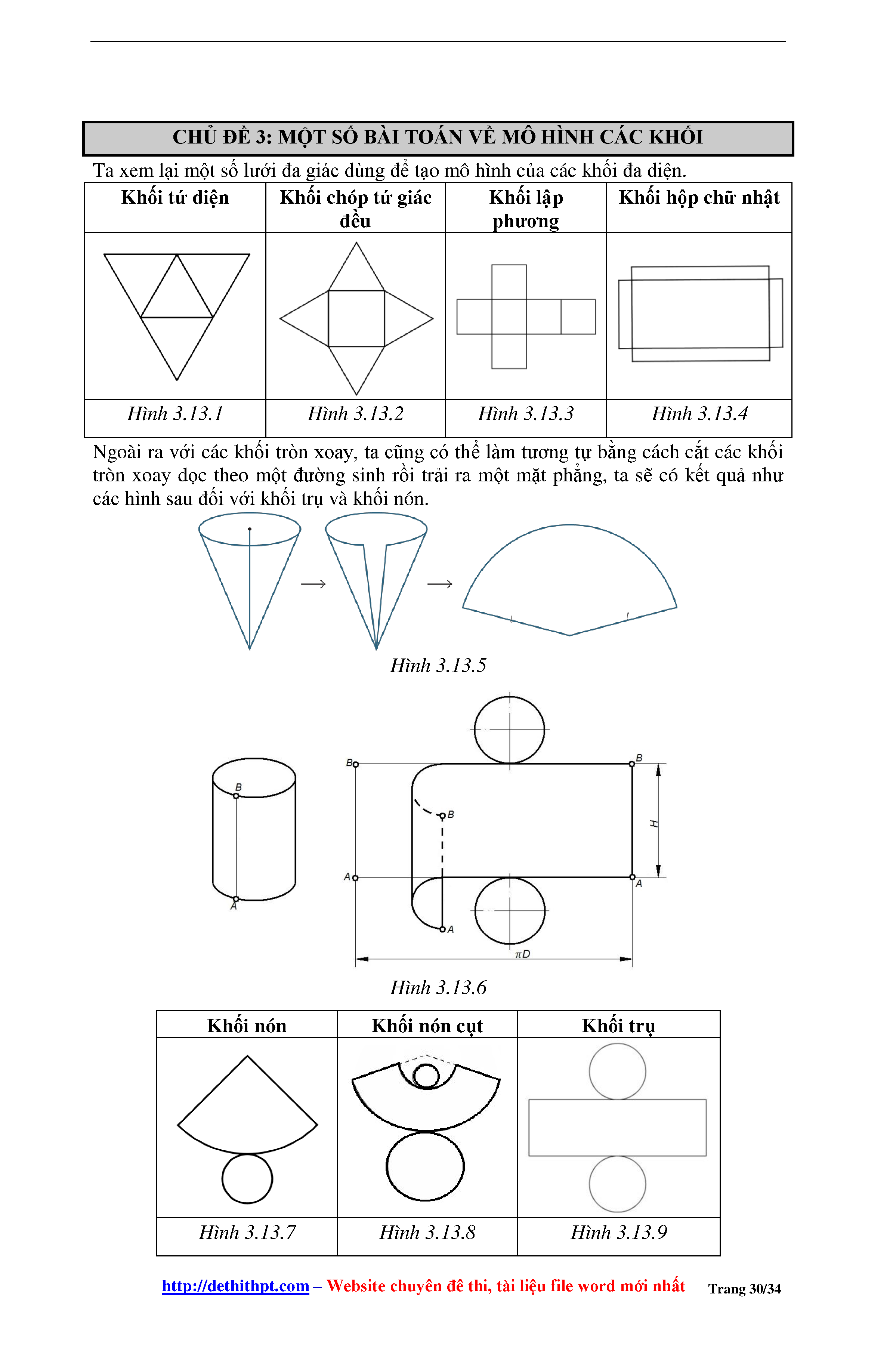
IV. Bản vẽ các khối đa diện

Các khối là các vật thể trong không gian với các kích thước gồm chiều dài, chiều rộng và chiều cao. Tuy nhiên, khi mô tả hình dạng của một khối, ta chỉ có thể biểu diễn khối đó trên giấy (hay trên 1 mặt phẳng).

Chính vì vậy, bản vẽ của khối đa diện là các hình biểu diễn của khối đa diện đó trong không gian lên giấy thông qua hình chiếu song song của vật thể theo một phương chiếu nhất định.

Để hiểu rõ hơn về về khối đa diện, các em có thể tham khảo thêm slide bên dưới